Research: Theory
Time Delay Systems

Time delay, commonly known as time difference of arrival or dead time, is an extensive phenomenon encountered in many different research areas such as unmanned air vehicles (UAVs), missiles, master-slave robots, haptic systems and biological systems. Leading causes of the time delay phenomena are the system dynamics, communication lines and networks, feedback structures and sensors. Current research from NCR involves designing novel, robust and adaptive controllers for uncertain nonlinear systems subject to known and unknown, constant and time dependent, input and state time delays, with additive disturbances.


Intelligent Control of Uncertain Nonlinear Systems

Improved control performance can result from including model knowledge of the system in the control design and stability analysis. Yet, there is some degree of uncertainty in most models of dynamic systems. Different tools may be required, based on the nature of the uncertainty. The focus of intelligent control is to understand how to incorporate different methods to compensate for the uncertainty. Efforts in this topic focus on methods such as

  • Extremum Seeking
  • Repetitive Learning Control
  • Neural Networks
  • Adaptive Control
  • and Biologically Inspired

to compensate for the uncertainty in the system. These approaches are in contrast to robust control methods that use high gain or high frequency components to reject uncertainty.


Intermittent Feedback

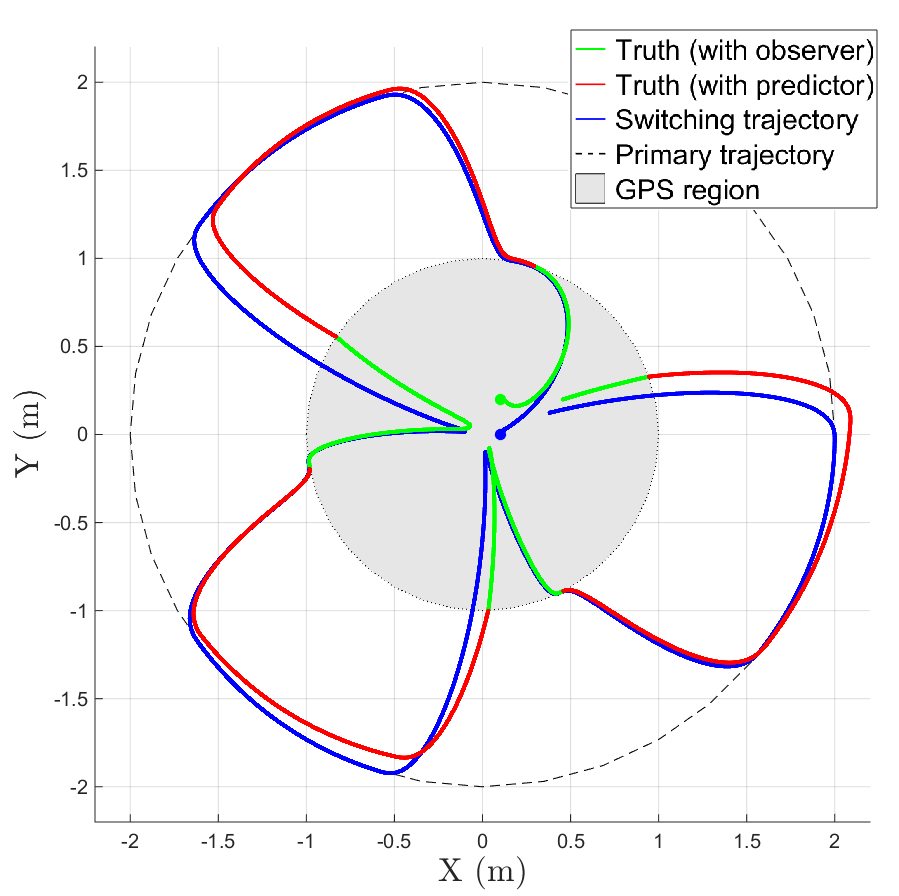
State feedback has been a core component in controller design of closed-loop control systems. With the use of closed-loop feedback control, control algorithms have been developed with robustness to uncertain system dynamics such as: parametric uncertainties, exogenous disturbances, and nonlinearities in the dynamics. However, factors such as the task definition, complex operating environments, or sensor modality can result in temporary losses (i.e., intermittencies) in state feedback. Due to these intermittencies, challenges arise in controller design and stability analysis. Motivated by such factors, NCR efforts have been made to develop solutions to relax the constant feedback constraint. Such solutions employ Lyapunov stability to develop dwell-time conditions to determine the time bounds in which a system can operate without feedback while remaining stable. For example, a simulation is shown in the figure where an agent is tasked with tracking a primary trajectory that is in a GPS denied region. To track the primary trajectory, the agent tracks a switching trajectory that leaves and re-enters the GPS region to ensure the dwell time conditions are met to ensure stability of the system. Additionally, further research has encompassed the use of intermittent feedback in areas such as: path-planning and path-following, hybrid-switched systems, and multi-agent systems.

Robust Integral of the Sign of the Error (RISE)

Robust Integral of the Sign of the Error (RISE) is a recently developed new differentiable high gain feedback control strategy that contains a unique integral signum term which can accommodate for sufficiently smooth bounded disturbances. A significant outcome of this new control structure is that asymptotic stability is obtained despite a fairly general uncertain disturbance. This technique can be used to develop a tracking controller for nonlinear systems in the presence of additive disturbances and parametric uncertainties under the assumption that the disturbances are C2 with bounded time derivatives. The fact that the RISE controller is continuous is especially useful from the implementation point of view. Other robust discontinuous feedback strategies are disadvantageous in that they require infinite bandwidth and cause chattering that may cause undesirable oscillations in the mechanical systems.


Optimal Control of Nonlinear Systems

Optimal control theory involves the design of controllers that can satisfy some tracking or regulation control objective while simultaneously minimizing some performance metric. A sufficient condition to solve an optimal control problem is to solve the Hamilton-Jacobi-Bellman (HJB) equation. For the special case of linear time-invariant systems, the solution to the HJB equation reduces to solving the algebraic Riccati equation. However, for general systems, the challenge is to find a value function that satisfies the HJB equation. Finding this value function has remained problematic because it requires the solution of a partial differential equation that can not be solved explicitly. NCR efforts focus on the development of data-based parametric approximation methods to approximate the unknown value function. These methods, also referred to as adaptive dynamic programming (ADP), depend on rich data to effectively approximate the value function over the operating domain. In traditional ADP methods, richness of the data correlates to the amount of excitation in the system typically introduced by adding exploration signals which makes hardware implementation difficult. NCR efforts focus on developing data-driven ADP techniques to alleviate the need for the addition of exploration signals, making hardware implementation viable. Another challenge in ADP is that traditional parametric methods in ADP rely on approximating the value function over the operating domain, which is computationally expensive. To overcome this challenge, NCR efforts also focus on developing computationally efficient ADP techniques which approximate the value function over a local neighborhood of the state which reduces the amount of unknown parameters in the problem. Further research has encompassed the use of ADP in areas such as

  • Regulation and monitoring of networked systems
  • Game-theory
  • Path-planning and path-following

    • and other applications where uncertainty and optimal control are at the root of the problem.


    Nonsmooth Systems

    For continuous systems, stability techniques such as the LaSalle-Yoshizawa Theorem provide a convenient analysis tool when the candidate Lyapunov function derivative is upper bounded by a negative semi-deļ¬nite function. However, adapting the LaSalle-Yoshizawa Theorem to systems where the time derivative of the system states are not locally Lipschitz remains an open problem. NCR efforts focus on generalized solutions for nonautonomous nonlinear systems with right-hand side discontinuities.


    Sponsors
    Ongoing Projects
    AFOSR: Center of Excellence in Assured Autonomy in Contested Environments
    NSF: Switched Adaptive Control Methods for Electrical Stimulation Induced Cycling
    AFOSR: A Switched Systems Approach for Navigation and Control with Intermittent Feedback
    NSF: Adaptive dynamic programming for uncertain nonlinear systems through coupling of nonlinear analysis and data-based learning
    ONR: Mine Counter Measure Path Planning and Optimal Control in Uncertain and Dynamic Maritime Environments

    Completed Projects
    NSF: Implicit Learning-Based Optimal Control of Uncertain Nonlinear Systems
    ONR: Adaptive Dynamic Programming for Autonomous Underwater Vehicles
    Related NCR Theory Publications