
Modular Adaptive Control of Wheeled Mobile Robots
Introduction
The position control problem of WMRs has been a heavily researched area due to both the challenging theoretical nature of the problem and its practical importance. Control researchers have targeted the problems of: Regulating the position/orientation of the WMR Tracking a time-varying reference trajectory (which includes the “path following” problem) Incorporating the effects of the dynamic model during the control design to enhance robustness Previous adaptive WMR research has exploited Lyapunov-based techniques; however, the Lyapunov-based approach tends to restrict the design of the adaptive update law Many of the previous adaptive controllers are restricted to utilizing position/velocity tracking error based gradient update laws. Motivated by the fact that gradient update laws often exhibit slow parameter convergence (may retard the transient performance), researchers have explored control designs for manipulators that incorporate other forms of update laws
Methodology
In this project, an adaptive torque control input for WMRs is developed to solve the unified tracking and regulation control problem. This result is achieved despite the presence of parametric uncertainty in the system dynamics. To compensate for parametric uncertainty in the system, a nonlinear damping based strategy is employed to provide input-to-state stability (ISS) of the controller. The ISS result yields a modular adaptive controller that allows the adaptive update law to be designed in a modular manner with respect to the feedback controller; hence, allowing for improved design flexibility. The structure of the kinematic controller is crucial to the development of the modular adaptive controller. Specifically, this approach is motivated by the fact that the kinematic controller is differentiable; thus, enabling integrator backstepping to incorporate the effects of the system dynamics. The approach ensures the transformed states of the system are negative-definite in the time derivative of a radially unbounded nonnegative function. This concept is a key advantage over many of the current WMR designs, which are negative semi-definite in the system states and require tools such as extended Barbalat's Lemma to prove stability, because it can be fused with nonlinear damping techniques to facilitate an ISS result.
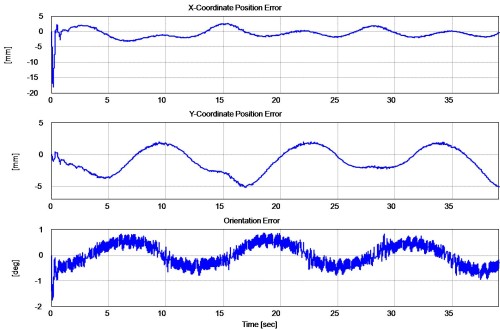
Gradient Update Law
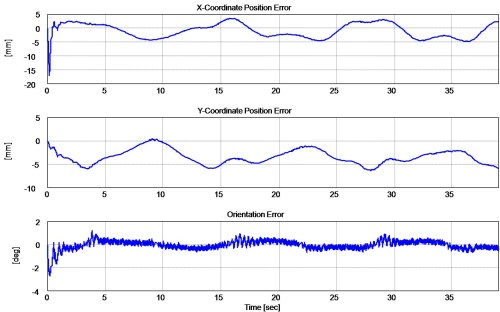
Least-Squares Update Law
Results
To highlight the modular nature of the adaptive controller, experimental results were obtained to demonstrate that the controller can be implemented with a prediction error based gradient update law and then implemented with the same control gains with a prediction error based least-squares update law to achieve similar performance
Publications
R. Brockett, “Asymptotic Stability and Feedback Stabilization”, Differential Geometric Control Theory, (R. Brockett., B. Millman, and H Sussmann Eds.), Birkhauser, Boston, 1983.
W.E. Dixon, D.M. Dawson, E. Zergeroglu, and A. Behal, Nonlinear Control of Wheeled Mobile Robots, Vol. 262 Lecture Notes in Control and Information Sciences, Springer-Verlag, 2000.
W. E. Dixon, M.S. de Queiroz, and D.M. Dawson, “Adaptive Tracking and Regulation of a Wheeled Mobile Robot with Controller/Update Law Modularity”, Proceedings of the 2002 IEEE International Conference on Robotics and Automation, Washington D.C., May 2002, pp. 2620-2625: see also IEEE Transactions on Control Systems Technology, to appear.
